La Recta de Euler

Una recta es un conjunto infinito de puntos que se encuentran alineados, están unidos y cuya longitud es infinita. Además, la dimensión 1 es aquella que está compuesta en su totalidad por una recta.

Pues bien, es de sobra conocido que para construir una recta hacen falta tan solo dos puntos, aunque como bien hemos mencionado antes contienen infinitos puntos y por lo tanto si tres puntos se encuentran alineados también formarán una recta.

Ortocentro:
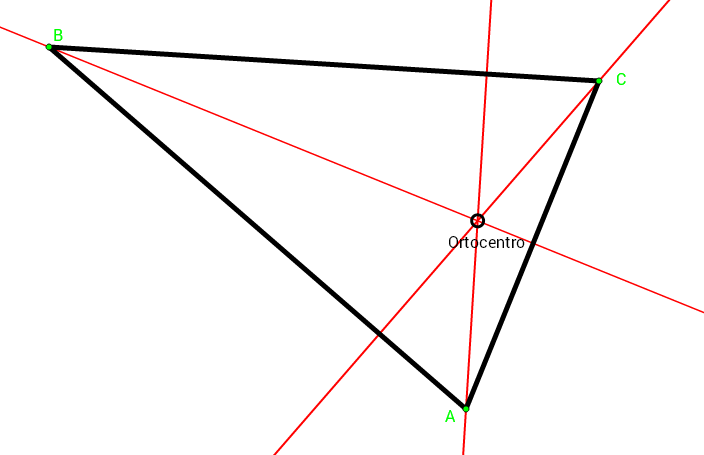
Es el punto de corte de las alturas de un triángulo. Las alturas son las rectas perpendiculares a cada lado que pasa por el vértice contrario.

Siempre estas tres rectas se cortan en un solo punto, cosa que no es tan trivial.

Baricentro:

Es el punto de corte de las medianas de un triángulo. Las medianas son las rectas que pasan por el centro de cada lado del triángulo y corta al vértice contrario.

Tampoco es trivial, pero estas tres rectas también se cortan siempre en un solo punto.

Circuncentro:

Es el punto de corte de las mediatrices de un triángulo. Las mediatrices son las rectas perpendiculares a cada lado y que pasan por el centro del mismo.

Como en los casos anteriores, solo se obtiene un punto.

Además, cuando se traza una circunferencia de centro circuncentro y radio hasta cualquiera de los vértices, se obtiene una circunferencia en la que está contenido el triángulo y además los vértices pertenecen a la propia circunferencia.

Pues ahora que ya conocemos a los protagonistas, se puede comprobar que siempre están alineados. En la imagen la Recta de Euler es la que está dibujada en amarillo y que efectivamente une los tres puntos anteriormente descritos.